Un día, discutiendo acerca de la forma exacta de un elefante, no conseguían ponerse de acuerdo. Como ninguno de ellos había tocado nunca uno, decidieron salir al día siguiente a la busca de un ejemplar, y así salir de dudas.
ESCRIBA LO QUE DESEA LEER EN ESTE BLOG
lunes, 7 de septiembre de 2015
Curva de Lévy C: cómo se usa los fractales para analizar hechos económicos
Curva de Lévy C
(Redirigido desde «Curva C de Lévy»)
En matemática, la curva de Lévy C es un fractal autosimilar. Descrita por primera vez por Ernesto Cesàro en 19061 y G. Farber en 1910,2 hoy lleva el nombre del matemático francés Paul Pierre Lévy quien, en 1938, fue el primero en exhibir sus propiedades de autosimilaridad y proveer una construcción geométrica.3
Construcción
Sistema-L
Utilizando un sistema de Lindenmayer, la construcción de la curva de Lévy C parte de un segmento de recta, este segmento se toma por la hipotenusa de un triángulo rectángulo isósceles, y se reemplaza por los dos catetos de dicho triángulo. De este modo, en esta etapa la curva consiste únicamente de dos segmentos de recta perpendiculares.
En la etapa siguiente, los dos segmentos son tomados como las hipotenusas de dos triángulos rectángulos isósceles, y se les reemplaza por los dos catetos correspondientes, y así sucesivamente.
Después de n etapas, la curva consistirá de 2n segmentos de recta, cada uno de longitud 2n/2 con respecto al segmento de partida.
El sistema de Lindenmayer asociado puede describirse entonces del siguiente modo:
En la etapa siguiente, los dos segmentos son tomados como las hipotenusas de dos triángulos rectángulos isósceles, y se les reemplaza por los dos catetos correspondientes, y así sucesivamente.
Después de n etapas, la curva consistirá de 2n segmentos de recta, cada uno de longitud 2n/2 con respecto al segmento de partida.
El sistema de Lindenmayer asociado puede describirse entonces del siguiente modo:
-
Variables: F Constantes: + − Inicio: F Reglas: F → +F−−F+
donde "F" significa "avanza recto", "+" significa "gira a la derecha 45°", y "−" significa "gira a la izquierda 45°". En el límite, el resultado de este proceso infinito es el fractal conocido como curva de Lévy C, dado su parecido con la letra C.
Variantes
Es posible construir variantes de esta curva utilizando ángulos diferentes de 45°, siempre y cuando sean menores a 60°.
Sistema IFS[editar]
La construcción de la curva de Lévy por medio de un sistema de funciones iteradas se basa en un conjunto de dosaplicaciones contractivas lineales de factor 1/√2. La primera introduce una rotación de 45°, y la segunda una rotación de -45°.
Propiedades
- La dimensión de Hausdorff de la curva es igual a 2 (contiene conjuntos abiertos).
- Su frontera tiene una dimensión estimada de 1.934007183Weisstein, Eric W. «LevyFractal». En Weisstein, Eric W.MathWorld (en inglés). Wolfram Research..
- Es un teselado del plano.4
- Es un caso particular de la curva de De Rham.
Véase también
Referencias
- Volver arriba↑ E. Cesaro, Fonctions continues sans dérivée, Archiv der Math. und Phys. 10 (1906) p. 57-63
- Volver arriba↑ G. Farber, Über stetige Funktionen II, Mathematische Annalen, 69 (1910) p. 372-443.
- Volver arriba↑ Paul Lévy, Plane or Space Curves and Surfaces Consisting of Parts Similar to the Whole (1938), reprinted in Classics on Fractals Gerald A. Edgar ed. (1993) Addison–Wesley, ISBN 0-201-58701-7
- Volver arriba↑ Le pavage du plan par la courbe de Lévy, Dubuc Serge & Li Jun
Enlaces externos
- Esta obra deriva de la traducción de Lévy C curve de Wikipedia en inglés, concretamente de esta versión, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported.
- VER MÁS
Vuelo de Lévy
Vuelo de Lévy
Un vuelo de Lévy, nombrado en honor al matemático francés Paul Pierre Lévy, es un tipo de paseo aleatorio en el cual los incrementos son distribuidos de acuerdo a unadistribución de probabilidad de cola pesada. Específicamente, la distribución usada es una ley potencial de la forma y = x -a donde 1 < a < 3 y por lo tanto tiene una varianzainfinita.
Los vuelos de Lévy son procesos de Márkov. Después de un gran número de pasos, la distancia del origen de la caminata al azar tiende a una distribución estable.
Los vuelos de Lévy de dos dimensiones fueron descritos por Benoît Mandelbrot en su libro The Fractal Geometry of Nature (La geometría fractal de la naturaleza). El escalamiento en forma de ley de potencias de las longitudes de pasos, da a los vuelos de Lévy una propiedad de escala invariante, es decir, la propiedad de un fractal.
Este método de simulación proviene fuertemente de las matemáticas relacionadas con la teoría del caos y es útil en la medida y las simulaciones estocásticas para los fenómenos naturales al azar o pseudoaleatorios. Los ejemplos incluyen análisis de datos de terremotos, matemáticas financieras, la criptografía, el análisis de señales así como muchas aplicaciones en astronomía, la biología, y la física.
Cuando los tiburones y otros depredadores del océano no pueden encontrar alimento, abandonan el movimiento browniano, el movimiento al azar visto en moléculas de gas, por el vuelo de Lévy —una mezcla de trayectorias largas y movimientos al azar cortos encontrados en líquidos turbulentos—. Los investigadores analizaron más de 12 millones de movimientos registrados durante 5.700 días en 55 animales marcados con un radio transmisor de 14 especies depredadoras del océano en los Océanos Atlánticos y Pacífico, incluyendo tiburones sedosos, atún de aleta amarilla, aguja azul y pez espada. Los datos mostraron que los vuelos de Lévy entremezclados con el movimiento browniano pueden describir los patrones de caza de los animales.1 2
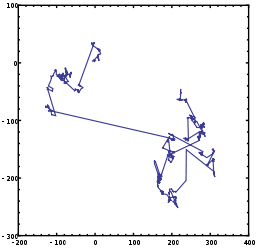
Cuadro 1. Un ejemplo de 1000 pasos de un vuelo de Lévy en dos dimensiones. El origen del movimiento está en [0.0], la dirección angular se distribuye uniformemente y el tamaño de paso está distribuido de acuerdo a la distribución de Lévy (es decir estable) con a=1 y ß=0 (es decir unadistribución de Cauchy). Observe la presencia de saltos grandes en la localización comparada al movimiento browniano ilustrado en el cuadro 2.

Cuadro 2. Un ejemplo de 1000 pasos de una aproximación a un tipo de movimiento browniano de vuelo de Lévy en dos dimensiones. El origen del movimiento está en [0, 0], la dirección angular está distribuida uniformemente y el tamaño del paso está distribuido según una distribución de Lévy (es decir estable) con a=2 y ß=0 (es decir un dedistribución normal).
Referencias[editar]
- Volver arriba↑ Discovery News - Sharks Have Math Skills
- Volver arriba↑ physicsworld.com - Sharks hunt via Lévy flights
Véase también[editar]
Suscribirse a:
Comentarios (Atom)


