.jpg) |
| Lloyd Shapley |
Este 15 de octubre, del año pasado, el Banco Central de Suecia otorgó el “Premio Nobel de Economía” a Lloyd Shapley y Alvin Roth.
Shapley es un matemático pionero de la teoría de juegos y Roth es un economista que amplió y aplicó las teorías del primero.
Shapley es un matemático pionero de la teoría de juegos y Roth es un economista que amplió y aplicó las teorías del primero.
Me parece que ambos investigadores no son ampliamente conocidos en las ramas que actualmente tienen mayor desarrollo dentro de la economía, pero si en algunos temas relacionados con la teoría de juegos y la intervención del Estado en la regulación o diseño de algunos mercados. En este post comentaremos brevemente algunos de los aportes de Shapley pues, debo reconocer que salvo un paper de Roth y Verrecchia1 sobre reparto de costos comunes en base al Valor de Shapley, no he leído los aportes más aplicados de Roth. De acuerdo a las referencias estos aportes se asocian con el rediseño de instituciones para un mejor funcionamiento, entre las que destacarían sistemas para que los nuevos médicos pudieran ser combinados los antiguos en los hospitales de forma más eficiente o el reparto de profesores con diferente rendimiento en diferentes aulas.
Shapley nació en 1923 en Cambridge, USA. Estudió en Princeton (donde hizo su tesis doctoral en matemáticas con el profesor Tucker) y trabajó en la Rand Corporation en la década del cuarenta y cincuenta, siendo durante muchos años profesor de la Universidad de California Los Angeles (UCLA) hasta su retiro. En sus inicios fue uno de los principales investigadores en teoría de juegos, habiendo escrito un paper sobre el juego de poker con John Nash, premio Nobel de economía en 1994 y famoso por la película y libro “Una Mente Brillante”. Es más, Lloyd Shapley sería uno de los amigos que apoyó a Nash para volver a enseñar luego de sus crisis de esquizofrenia.
El principal aporte de Shapley consistió en el famoso “Teorema del Valor de Shapley” (1953)1, el cual se encuentra dentro de la tradición de las primeras aplicaciones de la teoría de juegos en el marco de la teoría de Von Newman y Morgenstern, donde el enfoque era más bien buscar soluciones que cumplan con ciertos axiomas deseables para problemas donde hay varios agentes con diferentes intereses y aportes pero que pueden crear más valor cooperando entre ellos. Este enfoque alcanza incluso a las demostraciones del equilibrio general competitivo o al famoso teorema de imposibilidad de Kenneth Arrow. En el caso de Shapley, lo que se buscaba era “repartir” el valor que aportaba un agente a las diferentes coalisiones posibles de un juego cooperativo. Este esquema era particularmente importante como criterio normativo en los juegos que no tuvieran “núcleo” (es decir asignaciones no dominadas por otras para todos los agentes).
Shapley sugirió que se tomara una única imputación o asignación como preferible a las demás si cumplía con una serie de criterios deseables. Él demostró que existe una única imputación que cumple los siguientes criterios:
1) Que no dependa de las denominaciones
2) Que sea eficiente para el conjunto, es decir que reparta todo el valor generado por la coalisión
3) Que otorgue xi = 0 si “i” es inútil
4) Que un par de elecciones óptimas unidas den otra elección óptima
El teorema al que llegó es que la única función que cumplía con estos criterios era:
La idea era otorgar una suerte de suma ponderada de las posibles contribuciones del jugador i a las coaliciones de las que podría formar parte.
Donde:
PA = Probabilidad que el individuo i se ubique en un lugar s cualquiera para todas las posibles coaliciones que se puedan formar con s miembros.
PB = Probabilidad de que se forme una coalición de s-1 miembros sin el individuo i. Es decir, con un número máximo de n-1 miembros.
A modo de ejemplo, se puede tomar un caso típico de problema de reparto conocido como el problema del “Uso de la Tierra” 3, donde se tienen tres jugadores, un agricultor dueño de un terreno, un industrial y un urbanizador, tal que la función de valor del juego está caracterizada de la siguiente forma:
En este caso se puede calcular las asignaciones que corresponden al “núcleo” del juego, que tienen que cumplir con las condiciones de racionalidad grupal e individual:
Estas son diferentes a las imputaciones según la función de Shapley que serían las siguientes:
Análogamente se obtiene que:
Las aplicaciones de esta propuesta han sido diversas, como comentamos justamente le dieron el Nobel a Roth por este tipo de aportes. En mi caso particular, he llegado a ver algunos papers y tesis sobre el uso de este concepto para repartir costos comunes, en particular el costo de la transmisión de electricidad que no se puede recuperar con el pago en base al modelo marginalista. En este caso, la propuesta consiste en analizar “el uso” de cada usuario de las líneas de transmisión. Sin embargo, en este caso la propuesta compite con otras como la aplicación de “precios Ramsey” (aumentar los costos de los nodos en proporción inversa a la elasticidad de la demanda), criterios más ingenieriles y el reparto en base a beneficios.
Como se puede ver, la teoría de juegos cooperativos ahora no está dentro de las principales ramas de investigación de la economía pero ayudó en su momento a entender mejor muchos tipos de problemas. En particular, su auge se dio durante la guerra fría y los períodos donde el comercio internacional se analizaba en un sentido más restringido. Shapley es pues un heredero de este período y el enfoque de Von Newman, una de cuyas principales preocupaciones era encontrar analizar las condiciones de estabilidad y ausencia de conflicto luego de la segunda guerra mundial. Algo que uno siempre se pregunta cuando entregan los Nobel es sobre los otros investigadores que han estado muy cerca de los aportes, en este caso el que se habría quedado sería el profesor Martin Shubik, conocido por sus aportes en aplicaciones de la teoría de juegos a la economía política y la teoría del oligopolio.
Adjunto un link de una presentación que hiciera hace ya algunos años sobre este tema para los que quieran revisar algunos detalles de la notación y otros ejemplos (esta presentación está en deuda con Ramón García – Cobián quien en un curso de investigación de operaciones en la PUCP nos enseño a un grupo pequeño de alumnos los avances en juegos cooperativos):
Referencias
1 Alvin E. Roth y Robert E. Verrecchia (1979) The Shapley Value As Applied to Cost Allocation: A Reinterpretation: Journal of Accounting Research, Vol. 17, No. 1 (Spring, 1979), pp. 295-303
2 Shapley, Lloyd (1953) A Value for n-person Games [1953], en Contributions to the Theory of Games volumen II, H.W. Kuhn y A.W. Tucker (eds.).
3 Más detalles de este tipo de modelos se pueden ver en:
- Owen, Guillermo (1968) “Game Theory” New York: Academic Press.
- Mass-Collel A., M. D. Whinston and J. R. Green (1995) “Microeconomic Theory” Oxford University Press (Anexo A del capítulo 18).
4 Una de las primeras tesis en este campo fue:
- Contreras, Javier (1997) A Cooperative Game Theory Approach to Transmission Planning in Power Systems. Tesis doctoral en Ingeniería Eléctrica y Ciencias de la Computación. Universidad de California en Berkeley.


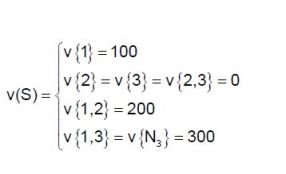



No hay comentarios:
Publicar un comentario